ESTADÍSTICA DESCRIPTIVA
DEFINICIÓN Y CLASIFICACIÓN DE VARIABLES
La estadística descriptiva es la rama de las Matemáticas que recolecta, presenta y caracteriza un
conjunto de datos (por ejemplo, edad de una población, altura de los estudiantes de una escuela,
temperatura en los meses de verano, etc.) con el fin de describir apropiadamente las diversas
características de ese conjunto.
Al conjunto de los distintos valores numéricos que adopta un carácter cuantitativo se llama variable
estadística.
Las variables pueden ser de dos tipos:
• Variables cualitativas o categóricas: no se pueden medir numéricamente (por ejemplo: nacionalidad,
color de la piel, sexo).
• Variables cuantitativas: tienen valor numérico (edad, precio de un producto, ingresos anuales).
Las variables también se pueden clasificar en:
• Variables unidimensionales: sólo recogen información sobre una característica (por ejemplo: edad de
los alumnos de una clase).
• Variables bidimensionales: recogen información sobre dos características de la población (por
ejemplo: edad y altura de los alumnos de una clase).
• Variables pluridimensionales: recogen información sobre tres o más características (por ejemplo:
edad, altura y peso de los alumnos de una clase).
Por su parte, las variables cuantitativas se pueden clasificar en discretas y continuas:
• Discretas: sólo pueden tomar valores enteros (1, 2, 8, -4, etc.). Por ejemplo: número de hermanos
(puede ser 1, 2, 3...., etc., pero, por ejemplo, nunca podrá ser 3.45).
• Continuas: pueden tomar cualquier valor real dentro de un intervalo. Por ejemplo, la velocidad de un
vehículo puede ser 90.4 km/h, 94.57 km/h...etc.
Cuando se estudia el comportamiento de una variable hay que distinguir los siguientes conceptos:
• Individuo: cualquier elemento que porte información sobre el fenómeno que se estudia. Así, si
estudiamos la altura de los niños de una clase, cada alumno es un individuo; si se estudia el precio
de la vivienda, cada vivienda es un individuo.
• Población: conjunto de todos los individuos (personas, objetos, animales, etc.) que porten información
sobre el fenómeno que se estudia. Por ejemplo, si se estudia el precio de la vivienda en una ciudad,
la población será el total de las viviendas de dicha ciudad.
• Muestra: subconjunto que seleccionado de una población. Por ejemplo, si se estudia el precio de la
vivienda de una ciudad, lo normal será no recoger información sobre todas las viviendas de la ciudad
DATOS. CLASIFICACIÓN, ORGANIZACIÓN Y CONSTRUCCIÓN DE BLOQUES
ESTADÍSTICOS
Los datos son medidas y/o números recopilados a partir de la observación. Los datos pueden concebirse
como información numérica necesaria para ayudar a tomar una decisión con más bases en una situación
particular.
Existen muchos métodos mediante los cuales se pueden obtener datos necesarios. Primero, se puede
buscar datos ya publicados por otras fuentes. Segundo, se puede diseñar un experimento. En tercer
lugar, se puede conducir un estudio. Cuarto, se pueden hacer observaciones del comportamiento,
actitudes u opiniones de los individuos en los que se está interesado.
Los datos se pueden clasificar en:
• Datos discretos. Son respuestas numéricas que surgen de un proceso de conteo.
• Datos continuos. Son respuestas numéricas que surgen de un proceso de medición.
ESCALAS DE MEDICIÓN
Medir en el campo de las ciencias exactas es comparar una magnitud con otra, tomada de manera
arbitraria como referencia, denominada patrón y expresar cuántas veces la contiene.
En el campo de las
ciencias sociales medir es “el proceso de vincular conceptos abstractos con indicadores empíricos”.
Al
resultado de medir lo se le llama medida.
La medición de las variables puede realizarse por medio de cuatro escalas de medición: la nominal,
ordinal, de intervalo y de razón. Se utilizan para ayudar en la clasificación de las variables, el diseño de
las preguntas para medir variables, e incluso indican el tipo de análisis estadístico apropiado para el
tratamiento de los datos.
Una característica esencial de la medición es la dependencia que tiene de la posibilidad de variación. La
validez y la confiabilidad de la medición de una variable depende de las decisiones que se tomen para
operarla y lograr una adecuada comprensión del concepto evitando imprecisiones y ambigüedades, en caso
contrario, la variable corre el riesgo inherente de ser invalidada debido a que no produce información
confiable.
a) Medición Nominal.
En este nivel de medición se establecen categorías distintivas que no implican un orden específico. Por
ejemplo, si la unidad de análisis es un grupo de personas, para clasificarlas se puede establecer la
categoría sexo con dos niveles, masculino (M) y femenino (F), los encuestados sólo tienen que señalar
su género, no se requiere de un orden real.
Así, se pueden asignar números a estas categorías para su identificación: 1=M, 2=F o bien, se pueden
invertir los números sin que afecte la medición: 1=F y 2=M. En resumen en la escala nominal se asignan
números a eventos con el propósito de identificarlos.
b) Medición Ordinal.
Se establecen categorías con dos o más niveles que implican un orden inherente entre si. La escala de
medición ordinal es cuantitativa porque permite ordenar a los eventos en función de la mayor o menor
posesión de un atributo o característica. Por ejemplo, en las instituciones escolares de nivel básico
suelen formar por estatura a los estudiantes, se desarrolla un orden cuantitativo pero no suministra
medidas de los sujetos. Estas escalas admiten la asignación de números en función de un orden
prescrito. Las formas más comunes de variables ordinales son ítems (reactivos) actitudinales
estableciendo una serie de niveles que expresan una actitud de acuerdo o desacuerdo con respecto a
algún referente. Por ejemplo, ante el reactivo: Pemex debe privatizarse, el respondiente puede marcar su
respuesta de acuerdo a las siguientes alternativas:
__ Totalmente de acuerdo
__ De acuerdo
__ Indiferente
__ En desacuerdo
__ Totalmente en desacuerdo
Las anteriores alternativas de respuesta pueden codificarse con números que van del uno al cinco que
sugieren un orden preestablecido pero no implican una distancia entre un número y otro.
c) Medición de Intervalo.
La medición de intervalo posee las características de la medición nominal y ordinal. Establece la distancia
entre una medida y otra. La escala de intervalo se aplica a variables continuas pero carece de un punto
cero absoluto. El ejemplo más representativo de este tipo de medición es un termómetro, cuando registra
cero grados centígrados de temperatura indica el nivel de congelación del agua y cuando registra 100
grados centígrados indica el nivel de ebullición, el punto cero es arbitrario no real, lo que significa que en
este punto no hay ausencia de temperatura.
d) Medición de Razón.
Una escala de medición de razón incluye las características de los tres anteriores niveles de medición
(nominal, ordinal e intervalo). Determina la distancia exacta entre los intervalos de una categoría.
Adicionalmente tiene un punto cero absoluto, es decir, en el punto cero no existe la característica o
atributo que se mide. Las variables de ingreso, edad, número de hijos, etc. son ejemplos de este tipo de
escala. El nivel de medición de razón se aplica tanto a variables continuas como discretas.
ORGANIZACIÓN DE DATOS
Muchas veces uno se pregunta, ¿para qué sirven las encuestas que a veces se hacen en la calle?,
¿Cómo saber si una estación de radio se escucha más que otra? , ¿Cuál candidato puede ganar? La
respuesta se comienza con la recaudación de datos.
Los datos son información que se recoge, esto puede ser opinión de las personas sobre un tema, edad o
sexo de encuestados, dónde viven, cuántas personas viven en una casa, qué tipo de sangre tiene un
grupo de personas, etc.
Hay datos que pueden ser de mucha utilidad a diferentes profesionales en la toma de decisiones, para
resolver problemas o para mostrar resultados de investigaciones. Una vez que se haya recogido toda la
información, se procede a crear una base de datos, donde se registran todos los datos obtenidos.
Algunas veces, si los datos son muy complicados, se codifican, esto quiere decir que se le coloca una
palabra clave que identifica un título muy largo. Cuando ya está elaborada la base de datos se parece a
una tabla.
Es importante recordar que nunca se colocan las tablas y las gráficas juntos, porque en realidad dicen lo
mismo, corrientemente se utiliza o una tabla y su análisis, o una gráfica y su análisis1
.
Por ejemplo, supóngase que se ha preguntado a un conjunto de n personas: ¿qué opinión tienen acerca
de la instalación de playas en la Ciudad de México en que el Gobierno del Distrito Federal ha hecho a
partir de 2007? Las n respuestas se encuentran en una escala que va de 1 a 9, donde 1 representa un
total desacuerdo con la medida mientras que 9 quiere significar un acuerdo total.
El resultado de la medición es el siguiente:
Tabla 1: Conjunto original de datos
7 5 6 8 6 5 9 5 8 6 5 7 5 5 4 5 8 5 4 2 6 6 4 6 4
8 4 3 4 3 3 1 4 5 6 5 8 5 4 7 4 3 5 3 4 9 4 2 6 3
4 2 4 1 3 6 3 1 2 4 4 6 2 4 7 4 2 4 6 4 4 6 7 5 8
5 7 6 5 6 5 7 5 6 4 5 4 1 6 5 6 5 5 5 4 6 2 5 5 6
5 4 4 3 5 5 9 4 3 6 5 7 3 2 4 4 7 4 2 1 8 2 7 4 5
5 7 5 5 1 5 8 5 6 7 6 6 7 7 5 2 5 6 5 8 5 3 6 5 5
Si se plantean las siguientes preguntas:
• ¿Cuántas personas fueron encuestadas?
• ¿Cuál fue la respuesta más frecuente?
• ¿Cuántas personas tienen, como máximo, una actitud de cuatro puntos en la escala? (es decir,
¿cuántas personas se encuentran en desacuerdo con la medida?)
Es difícil responder a las tres cuestiones. ¿Cuál es el problema?
Las personas tienen dificultades para procesar o tener en cuenta mucha información de forma
simultanea. La tabla 1 muestra demasiados datos y es preciso contar con mucha paciencia y una buena
vista para responder a las preguntas anteriores con seguridad.
Así pues, ¿qué se puede hacer? Una solución alternativa al repaso repetitivo de la tabla 1 es organizar
los datos de tal forma que tengan una disposición que facilite la lectura. En este sentido, la primera
acción a realizar es ordenar los datos desde el que posee el valor más pequeño hasta el que cuenta con
el valor mayor.
Obsérvese el resultado:
Tabla 2: Conjunto ordenado de datos
1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3
4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4
5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5 5
6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6 6
7 7 7 7 7 7 7 7 7 7 7 7 7 7 8 8 8 8 8 8 8 8 8 9 9 9
Se logra una ganancia al pasar de la tabla 1 a la tabla 2. Parece que ésta es más fácil de interpretar. No
ha desaparecido ninguna información, el único cambio está en su ordenación. No obstante, la solución es
parcial, puesto que aún debe ser mejorada (sigue siendo difícil responder a las preguntas).
Generalmente, el titulo de la tabla va encima de ésta, mientras que el título de una figura va por debajo. El título, de ambas, sólo
lleva la primera palabra en mayúscula y no va subrayado.
 |
DIAGRAMA DE SECTORES   MEDIDAS DE TENDENCIA CENTRAL  NOCIONES BÁSICAS DE PROBABILIDAD Dos enfoques objetivos para responder a cómo se obtiene la probabilidad de un suceso que presuponen que la probabilidad de un suceso es un dato objetivo que la persona conoce o no: • Probabilidad de un suceso aleatorio (S): cociente entre el número de resultados favorables del suceso aleatorio y el número total de resultados posibles • Probabilidad de un suceso: frecuencia relativa del mismo después de haberlo repetido un número razonablemente grande de veces Procedimientos que sirven para juegos de azar pero no tanto en la vida diaria; por eso se utilizan las probabilidades subjetivas: derivadas de la información a disposición o las creencias u opiniones del individuo. Según la teoría de la probabilidad, la probabilidad debe seguir los siguientes axiomas: • la probabilidad de un suceso es igual o mayor que 0. No existen probabilidades negativas. • la probabilidad de un suceso seguro es 1. La probabilidad de no ocurrencia es: P(no S)= 1 – P(S) • si dos sucesos (S1y S2) son mutuamente excluyentes entre sí, la probabilidad de uno u otro será igual a la suma de sus probabilidades: P(S1ó S2) = P(S1)+ P(S2) EL RAZONAMIENTO PROBABILÍSTICO
Se ignora la capacidad predictiva del dato: fijarse sólo en la información que está
presente en una situación concreta, olvidándose del resto.
1) SESGO DE EXPLICACIÓN: estimar como más probable aquello que ha sido
explicado previamente. Pedir a unos sujetos que expliquen por qué determinado
candidato electoral debía resultar elegido, estos asignaron mayor probabilidad
de éxito electoral a dicho candidato, tan sólo con haber imaginado el
escenario de triunfo electoral
2) SESGO RETROSPECTIVO: probabilidad percibida de un suceso aumenta cdo los sujetos conocen el resultado final. Se preguntó a unos sujetos qué cosas, de una lista ofrecida, era probable que ocurriesen en el próximo viaje de Nixon a China y, posteriormente a haberse producido este, se les volvió a preguntar por las mismas. Los sujetos cambiaron sus estimaciones iniciales ajustándolas a lo que realmente había sucedido. 3) SESGO DE LA CORRELACIÓN ILUSORIA: dos sucesos altamente significativos o distintivos se asocian, dicha asociación queda establecida en la memoria y es más accesible y fácil de recordar, por lo que se estima mucho más frecuente de lo que en realidad es. Creación de estereotipos sociales. C) HEURÍSTICO DE ANCLAJE Y AJUSTE Emisión de un juicio basado en algún valor inicial (obtenido mediante cualquier procedimiento, incluido el azar) que posteriormente se va ajustando, a medida que se añade más información, hasta producir la respuesta final. La persona realizaría el juicio a partir de alguno de los rasgos del estímulo, y posteriormente, se ajustaría este primer juicio para que integre los rasgos restantes. Por tanto, la respuesta final estará sesgada hacia el valor inicial, tanto si es relevante para el problema como si no lo es. Hay varios ejemplos en las páginas 347 y 348; uno de ellos es pedir a los sujetos que estimen la proporción de población negra en EE.UU. mostrando previamente un número al azar y cada grupo ajusto su juicio a los valores iniciales ofrecidos. D) CRÍTICAS DE LOS HEURÍSTICOS • Flexibilidad: El mismo heurístico se utiliza en situaciones muy diferentes sin poder determinar cuáles son sus condiciones de aplicación; no se puede predecir cuál heurístico se aplicará en una situación concreta. Posiblemente se utilicen sucesivamente, considerando primero la información más accesible y seleccionando luego la más representativa. Distintos heurísticos se utilizan para explicar la misma situación; algunos sesgos pueden ser debidos tanto a uno como a otro heurístico. El mejor definido de los tres heurísticos es el de representatividad, seguido del de accesibilidad y por último el de anclaje. Leyes de la probabilidad
La probabilidad es un método por el cual se obtiene la frecuencia de un suceso determinado mediante la realización de un experimento aleatorio, del que se conocen todos los resultados posibles, bajo condiciones suficientemente estables. La teoria de la probabilidad se usa extensamente en áreas como la estadistica, la fisica, la matematicas, las ciencias y la filosofia para sacar conclusiones sobre la probabilidad discreta de sucesos potenciales y la mecánica subyacente discreta de sistemas complejos.
La probabilidad constituye un importante parámetro en la determinación de las diversas casualidades obtenidas tras una serie de eventos esperados dentro de un rango estadístico.
Existen diversas formas como método abstracto, como la teoria de dempster y la teoria de la relatividad numerica, esta última con un alto grado de aceptación si se toma en cuenta que disminuye considerablemente las posibilidades hasta un nivel mínimo ya que somete a todas las antiguas reglas a una simple ley de relatividad.
La probabilidad de un evento se denota con la letra p y se expresa en términos de una fracción y no en porcentajes, por lo que el valor de p cae entre 0 y 1. Por otra parte, la probabilidad de que un evento “no ocurra” equivale a 1 menos el valor de p y se denota con la letra q
Los tres métodos para calcular las probabilidades son la regla de la adición, la regla de la multiplicación.
 Regla de la adición
La regla de la adición o regla de la suma establece que la probabilidad de ocurrencia de cualquier evento en particular es igual a la suma de las probabilidades individuales, si es que los eventos son mutuamente excluyentes, es decir, que dos no pueden ocurrir al mismo tiempo.
P(A o B) = P(A) U P(B) = P(A) + P(B) si A y B son mutuamente excluyente. P(A o B) = P(A) + P(B) − P(A y B) si A y B son no excluyentes.
Siendo: P(A) = probabilidad de ocurrencia del evento A. P(B) = probabilidad de ocurrencia del evento B. P(A y B) = probabilidad de ocurrencia simultánea de los eventos A y B.
Regla de la multiplicación
La regla de la multiplicación establece que la probabilidad de ocurrencia de dos o más eventos estadísticamente independientes es igual al producto de sus probabilidades individuales.
P(A y B) = P(A B) = P(A)P(B) si A y B son independientes. P(A y B) = P(A B) = P(A)P(B|A) si A y B son dependientes
La regla de Laplace establece que:
Para aplicar la regla de Laplace es necesario que los experimentos den lugar a sucesos equiprobables, es decir, que todos tengan o posean la misma probabilidad.
P(A) = Nº de casos favorables / Nº de resultados posibles
Esto significa que: la probabilidad del evento A es igual al cocientedel número de casos favorables (los casos dónde sucede A) sobre el total de casos posibles.-
-Aplicacion:
Dos aplicaciones principales de la teoría de la probabilidad en el día a día son en el análisis de riesgo y en el comercio de los mercados de materias. Los gobiernos normalmente aplican métodos probabilísticos en regulacion ambiental donde se les llama “analisis de vias de dispercion”, y a menudo miden el bienestar usando métodos que son estocásticos por naturaleza, y escogen qué proyectos emprender basándose en análisis estadísticos de su probable efecto en la población como un conjunto. No es correcto decir que la estadistica está incluida en el propio modelado, ya que típicamente los análisis de riesgo son para una única vez y por lo tanto requieren más modelos de probabilidad fundamentales, por ej. “la probabilidad de otro 11-S”. Una ley de numeros pequeños tiende a aplicarse a todas aquellas elecciones y percepciones del efecto de estas elecciones, lo que hace de las medidas probabilísticas un tema político.
Un buen ejemplo es el efecto de la probabilidad percibida de cualquier conflicto generalizado sobre los precios del petróleo en Oriente Medio – que producen un efecto dominó en la economía en conjunto. Un cálculo por un mercado de materias primas en que la guerra es más probable en contra de menos probable probablemente envía los precios hacia arriba o hacia abajo e indica a otros comerciantes esa opinión. Por consiguiente, las probabilidades no se calculan independientemente y tampoco son necesariamente muy racionales. La teoría de las fiansas conducyuales surgió para describir el efecto de este pensamiento de grupo en el precio, en la política, y en la paz y en los conflictos.
Se puede decir razonablemente que el descubrimiento de métodos rigurosos para calcular y combinar los cálculos de probabilidad ha tenido un profundo efecto en la sociedad moderna. Por consiguiente, puede ser de alguna importancia para la mayoría de los ciudadanos entender cómo se calculan los pronósticos y las probabilidades, y cómo contribuyen a la reputación y a las decisiones, especialmente en una democracia.
Otra aplicación significativa de la teoría de la probabilidad en el día a día es en la fiabilidad. Muchos bienes de consumo, como los automoviles y la electrónica de consumo, utilizan la teoria de la fiabilidad en el diseño del producto para reducir la probabilidad de avería. La probabilidad de avería también está estrechamente relacionada con la garantia del producto.
El teorema de Bayes parte de una situación en la que es posible conocer las probabilidades de que ocurran una serie de sucesos Ai.
A esta se añade un suceso B cuya ocurrencia proporciona cierta información, porque las probabilidades de ocurrencia de B son distintas según el suceso Ai que haya ocurrido.
Conociendo que ha ocurrido el suceso B, la fórmula del teorema de Bayes nos indica como modifica esta información las probabilidades de los sucesos Ai.
Ejemplo: Si seleccionamos una persona al azar, la probabilidad de que sea diabética es 0,03. Obviamente la probabilidad de que no lo sea es 0,97.
Si no disponemos de información adicional nada más podemos decir, pero supongamos que al realizar un análisis de sangre los niveles de glucosa son superiores a 1.000 mg/l, lo que ocurre en el 95% de los diabéticos y sólo en un 2% de las personas sanas.
¿Cuál será ahora la probabilidad de que esa persona sea diabética?
La respuesta que nos dá el teorema de bayes es que esa información adicional hace que la probabilidad sea ahora 0,595.
Vemos así que la información proporcionada por el análisis de sangre hace pasar, la probabilidad inicial de padecer diabetes de 0,03, a 0,595. Evidentemente si la prueba del análisis de sangre hubiese sido negativa, esta información modificaría las probabilidades en sentido contrario. En este caso la probabilidad de padecer diabetes se reduciría a 0,0016.  ESPERANZA Y VARIANZA
Los nombres de esperanza matemática y valor esperado tienen su origen en los juegos de azar y hacen referencia a la ganancia promedio esperada por un jugador cuando hace un gran número de apuestas.
Si la esperanza matemática es cero, E(x) = 0, el juego es equitativo, es decir, no existe ventaja ni para el jugador ni para la banca.
Ejemplos
Si una persona compra una papeleta en una rifa, en la que puede ganar de 5.000 € ó un segundo premio de 2000 € con probabilidades de: 0.001 y 0.003. ¿Cuál sería el precio justo a pagar por la papeleta?
E(x) = 5000 · 0.001 + 2000 · 0.003 = 11 €
Un jugador lanza dos monedas. Gana 1 ó 2 € si aparecen una o dos caras. Por otra parte pierde 5 € si no aparece cara. Determinar la esperanza matemática del juego y si éste es favorable.
E = {(c,c);(c,x);(x,c);(x,x)}
p(+1) = 2/4
p(+2) = 1/4
p(−5) = 1/4
E(x)= 1 · 2/4 + 2 · 1/4 - 5 · 1/4 = −1/4.
Es desfavorable
Desviación estándar
La desviación estándar (σ) mide cuánto se separan los datos.
La fórmula es fácil: es la raíz cuadrada de la varianza. Así que, "¿qué es la varianza?"
Varianza
La varianza (que es el cuadrado de la desviación estándar: σ2) se define así:
Es la media de las diferencias con la media elevadas al cuadrado.
En otras palabras, sigue estos pasos:
EJEMPLO
Tú y tus amigos han medido las alturas de sus perros (en milímetros):
Las alturas (de los hombros) son: 600mm, 470mm, 170mm, 430mm y 300mm.Calcula la media, la varianza y la desviación estándar.
DISTRIBUCIÓN DE POISSON
Esta distribución es una de las más importantes distribuciones de variable discreta. Sus principales aplicaciones hacen referencia a la modelización de situaciones en las que nos interesa determinar el número de hechos de cierto tipo que se pueden producir en un intervalo de tiempo o de espacio, bajo presupuestos de aleatoriedad y ciertas circunstancias restrictivas. Otro de sus usos frecuentes es la consideración límite de procesos dicotómicos reiterados un gran número de veces si la probabilidad de obtener un éxito es muy pequeña .
Proceso experimental del que se puede hacer derivar
Esta distribución se puede hacer derivar de un proceso experimental de observación en el que tengamos las siguientes características
· Se observa la realización de hechos de cierto tipo durante un cierto periodo de tiempo o a lo largo de un espacio de observación
· Los hechos a observar tienen naturaleza aleatoria ; pueden producirse o no de una manera no determinística.
· La probabilidad de que se produzcan un número x de éxitos en un intervalo de amplitud t no depende del origen del intervalo (Aunque, sí de su amplitud)
· La probabilidad de que ocurra un hecho en un intervalo infinitésimo es prácticamente proporcional a la amplitud del intervalo.
· La probabilidad de que se produzcan 2 o más hechos en un intervalo infinitésimo es un infinitésimo de orden superior a dos.
En consecuencia, en un intervalo infinitésimo podrán producirse O ó 1 hecho pero nunca más de uno
· Si en estas circunstancias aleatorizamos de forma que la variable aleatoria X signifique o designe el "número de hechos que se producen en un intervalo de tiempo o de espacio", la variable X se distribuye con una distribución de parámetro l . Así :
El parámetro de la distribución es, en principio, el factor de proporcionalidad para la probabilidad de un hecho en un intervalo infinitésimo. Se le suele designar como parámetro de intensidad , aunque más tarde veremos que se corresponde con el número medio de hechos que cabe esperar que se produzcan en un intervalo unitario (media de la distribución); y que también coincide con la varianza de la distribución.
Por otro lado es evidente que se trata de un modelo discreto y que el campo de variación de la variable será el conjunto de los número naturales, incluido el cero:
Función de cuantía
A partir de las hipótesis del proceso, se obtiene una ecuación diferencial de definición del mismo que puede integrarse con facilidad para obtener la función de cuantía de la variable "número de hechos que ocurren en un intervalo unitario de tiempo o espacio "
Que sería :
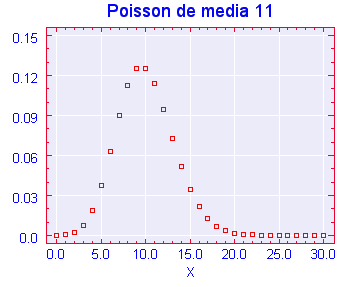
Cuya representación gráfica para un modelo de media 11 sería la adjunta .
Obsérvense los valores próximos en la media y su forma parecida a la campana de Gauss , en definitiva , a la distribución normal
La función de distribución vendrá dada por :
Función Generatriz de Momentos
Su expresión será :

dado que
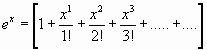 tendremos que tendremos que
luego :
Para la obtención de la media y la varianza aplicaríamos la F.G.M.; derivándola sucesivamente e igualando t a cero .
Así.
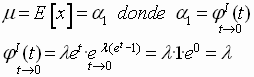
Una vez obtenida la media , obtendríamos la varianza en base a :
haciendo t = 0
por lo que
así se observa que media y varianza coinciden con el parámetro del modelo siendo , l
En cuanto a la moda del modelo tendremos que será el valor de la variable que tenga mayor probabilidad , por tanto si Mo es el valor modal se cumplirá que :
Y, en particular:
A partir de estas dos desigualdades, es muy sencillo probar que la moda tiene que verificar:
Podemos observar cómo el intervalo al que debe pertenecer la moda tiene una amplitud de una unidad , de manera que la única posibilidad de que una distribución tenga dos modas será que los extremos de este intervalo sean números naturales, o lo que es lo mismo que el parámetro l sea entero, en cuyo caso las dos modas serán l -1 y l .
La distribución de Poisson verifica el teorema de adición para el parámetro l .
"La variable suma de dos o más variables independientes que tengan una distribución de Poisson de distintos parámetros l (de distintas medias) se distribuirá, también con una distribución de Poisson con parámetro l la suma de los parámetros l (con media, la suma de las medias) :
En efecto:
Sean x e y dos variables aleatorias que se distribuyen con dos distribuciones de Poisson de distintos parámetros siendo además x e y independientes
Así
Debemos probar que la variable Z= x+y seguirá una Poisson con parámetro igual a la suma de los de ambas:
En base a las F.G.M para X
Para Y
De manera que la función generatriz de momentos de Z será el producto de ambas ya que son independientes :
Siendo
Convergencia de la distribución binomial a la Poisson
Se puede probar que la distribución binomial tiende a converger a la distribución de Poisson cuando el parámetro n tiende a infinito y el parámetro p tiende a ser cero, de manera que el producto de n por p sea una cantidad constante. De ocurrir esto la distribución binomial tiende a un modelo de Poisson de parámetro l igual a n por p
Este resultado es importante a la hora del cálculo de probabilidades , o , incluso a la hora de inferir características de la distribución binomial cuando el número de pruebas sea muy grande
El resultado se prueba , comprobando como la función de cuantía de una distribución binomial con
En efecto : la función de cuantía de la binomial es
Y llamamos
 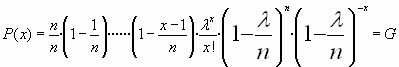
realizando
Fuente: https://www.uv.es/ceaces/base/modelos%20de%20probabilidad/poisson.htm http://www.ugr.es/~jsalinas/bayes.htm https://dddonnita.wordpress.com/leyes-de-la-probabilidad/
ELABORADO
POR:
EDGAR ROLANDO XAR COROY CARNÉ: 161000184 INGENIERÍA INDUSTRIAL IV SEMESTRE, DOMINGO ESTADISTICA 1 |





Comentarios
Publicar un comentario